协方差矩阵

1.协方差定义

X、Y是两个随机变量，X、Y的协方差cov(X,Y)定义为：

其中

2.协方差矩阵定义

矩阵中的数据按行排列和按列排列求出的协方差矩阵是不同的，这里默认是按行排列，即每一行是一个sample，那么每一列就是一个随机变量。

协方差矩阵：

协方差矩阵的维度等于随机变量的个数，即每一个sample的维度。在某些场合前边也会出现,而不是。

3.求解协方差矩阵的步骤

例子

则X表示x轴可能出现的数，Y表示y轴可能出现的数。

注意：给定这4个样本，每个样本都是二维的，只有X和Y两个维度

所以：

即：

协方差(i,j)=（每i列的所有元素-每i列的均值）*(每j列的所有元素-每j列的均值)

这里只有X,Y两列，所以得到的协方差矩阵是2*2的矩阵，下面分别求出每一个元素：

所以，按照定义，给定的4个二维样本的协方差矩阵为：

用matlab计算这个例子：

z=[1,2;3,6;4,2;5,2]

cov(z)

ans=

可以看出，matlab计算协方差过程中还将元素统一缩小了3倍。所以，协方差的matlab计算公式为：

协方差(i,j)=（每i列的所有元素-每i列的均值）*(每j列的所有元素-每j列的均值)/(样本数-1)

又一例子

则

解：
（1）第一列均值为2，第二列为3，第三列为1.67，第四列为3.33

(2)计算公式：

以举例：

4.协方差代表的意义

在概率论中，两个随机变量 X 与 Y 之间相互关系，大致有下列3种情况：

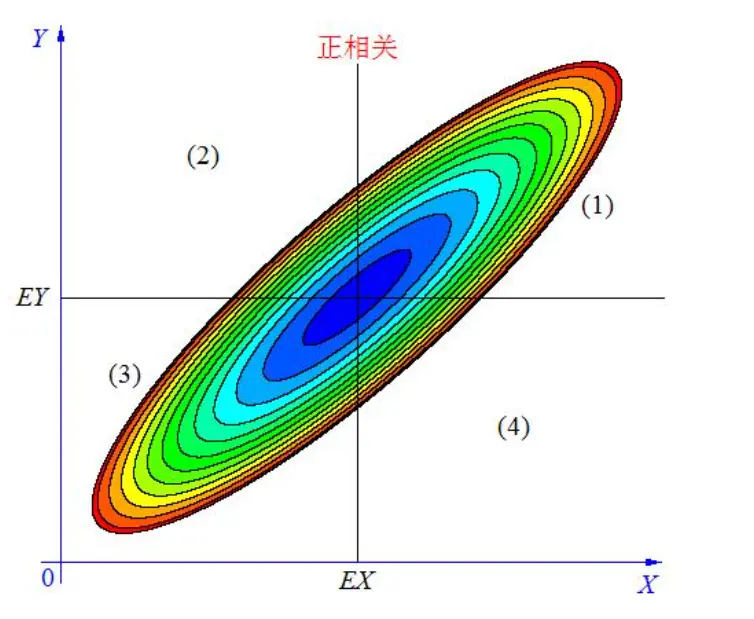
情况一,如上, 当 X, Y 的联合分布像上图那样时，我们可以看出，大致上有： X 越大 Y 也越大， X 越小 Y 也越小，这种情况，我们称为“正相关”。

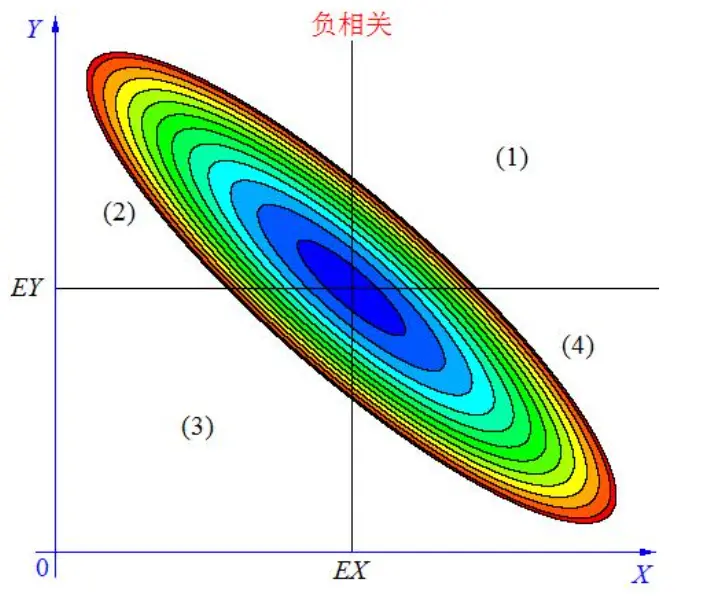
情况二, 如上图, 当X, Y 的联合分布像上图那样时，我们可以看出，大致上有：X 越大Y 反而越小，X 越小 Y 反而越大，这种情况，我们称为“负相关”。

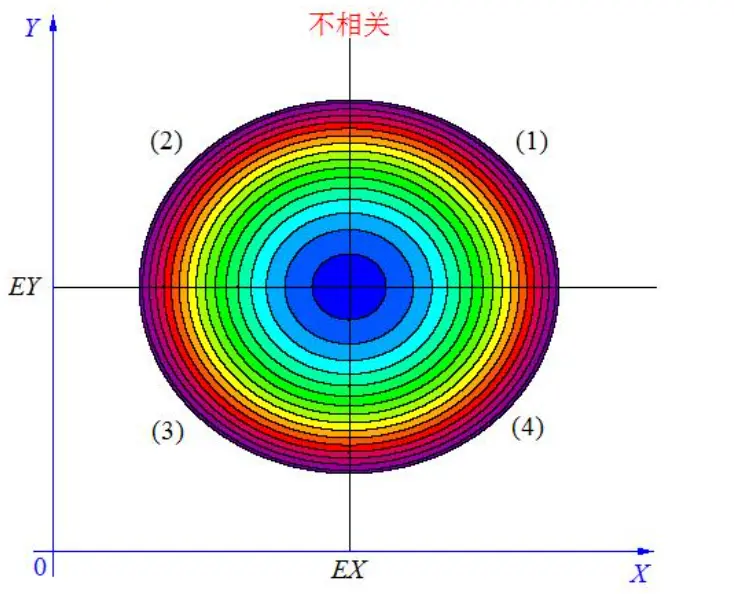
情况三,如上图, 当X, Y 的联合分布像上图那样时，我们可以看出：既不是X 越大Y 也越大，也不是 X 越大 Y 反而越小，这种情况我们称为“不相关”。

---

怎样将这3种相关情况，用一个简单的数字表达出来呢？

在图中的区域（1）中，有 X> ，Y- >0 ，所以(X-)(Y-)>0；

在图中的区域（2）中，有 X< ，Y->0 ，所以(X-)(Y-)<0；

在图中的区域（3）中，有 X< ，Y-<0 ，所以(X-)(Y-)>0；

在图中的区域（4）中，有 X> ，Y-<0 ，所以(X-)(Y-)<0。

当X与Y正相关时，它们的分布大部分在区域（1）和（3）中，小部分在区域（2）和（4）中，所以平均来说，有E(X-)(Y-)>0

当 X与 Y负相关时，它们的分布大部分在区域（2）和（4）中，小部分在区域（1）和（3）中，所以平均来说，有(X-)(Y-)<0

当 X与 Y不相关时，它们在区域（1）和（3）中的分布，与在区域（2）和（4）中的分布几乎一样多，所以平均来说，有(X-)(Y-)=0

所以，我们可以定义一个表示X, Y 相互关系的数字特征，也就是协方差

cov(X, Y) = E(X-)(Y-)

当cov(X, Y)>0时，表明X与Y正相关；

当cov(X, Y)<0时，表明X与Y负相关；

当 cov(X, Y)=0时，表明X与Y不相关。

这就是协方差的意义。