05 | 语法分析(三):实现一门简单的脚本语言

讲述:宫文学
时长13:37大小12.48M
前两节课结束后,我们已经掌握了表达式的解析,并通过一个简单的解释器实现了公式的计算。但这个解释器还是比较简单的,看上去还不大像一门语言。那么如何让它支持更多的功能,更像一门脚本语言呢?本节课,我会带你寻找答案。
我将继续带你实现一些功能,比如:
- 支持变量声明和初始化语句,就像“int age” “int age = 45”和“int age = 17+8+20”;
- 支持赋值语句“age = 45”;
- 在表达式中可以使用变量,例如“age + 10 *2”;
- 实现一个命令行终端,能够读取输入的语句并输出结果。
实现这些功能之后,我们的成果会更像一个脚本解释器。而且在这个过程中,我还会带你巩固语法分析中的递归下降算法,和你一起讨论“回溯”这个特征,让你对递归下降算法的特征理解得更加全面。
不过,为了实现这些新的语法,我们首先要把它们用语法规则描述出来。
增加所需要的语法规则
首先,一门脚本语言是要支持语句的,比如变量声明语句、赋值语句等等。单独一个表达式,也可以视为语句,叫做“表达式语句”。你在终端里输入 2+3;,就能回显出 5 来,这就是表达式作为一个语句在执行。按照我们的语法,无非是在表达式后面多了个分号而已。C 语言和 Java 都会采用分号作为语句结尾的标识,我们也可以这样写。
我们用扩展巴科斯范式(EBNF)写出下面的语法规则:
变量声明语句以 int 开头,后面跟标识符,然后有可选的初始化部分,也就是一个等号和一个表达式,最后再加分号:
表达式语句目前只支持加法表达式,未来可以加其他的表达式,比如条件表达式,它后面同样加分号:
赋值语句是标识符后面跟着等号和一个表达式,再加分号:
为了在表达式中可以使用变量,我们还需要把 primaryExpression 改写,除了包含整型字面量以外,还要包含标识符和用括号括起来的表达式:
这样,我们就把想实现的语法特性,都用语法规则表达出来了。接下来,我们就一步一步实现这些特性。
让脚本语言支持变量
之前实现的公式计算器只支持了数字字面量的运算,如果能在表达式中用上变量,会更有用,比如能够执行下面两句:
这两个语句里面的语法特性包含了变量声明、给变量赋值,以及在表达式里引用变量。为了给变量赋值,我们必须在脚本语言的解释器中开辟一个存储区,记录不同的变量和它们的值:
我们简单地用了一个 HashMap 作为变量存储区。在变量声明语句和赋值语句里,都可以修改这个变量存储区中的数据,而获取变量值可以采用下面的代码:
通过这样的一个简单的存储机制,我们就能支持变量了。当然,这个存储机制可能过于简单了,我们后面讲到作用域的时候,这么简单的存储机制根本不够。不过目前我们先这么用着,以后再考虑改进它。
解析赋值语句
接下来,我们来解析赋值语句,例如“age = age + 10 * 2;”:
为了方便你理解,我来解读一下上面这段代码的逻辑:
我们既然想要匹配一个赋值语句,那么首先应该看看第一个 Token 是不是标识符。如果不是,那么就返回 null,匹配失败。如果第一个 Token 确实是标识符,我们就把它消耗掉,接着看后面跟着的是不是等号。如果不是等号,那证明我们这个不是一个赋值语句,可能是一个表达式什么的。那么我们就要回退刚才消耗掉的 Token,就像什么都没有发生过一样,并且返回 null。回退的时候调用的方法就是 unread()。
如果后面跟着的确实是等号,那么在继续看后面是不是一个表达式,表达式后面跟着的是不是分号。如果不是,就报错就好了。这样就完成了对赋值语句的解析。
利用上面的代码,我们还可以改造一下变量声明语句中对变量初始化的部分,让它在初始化的时候支持表达式,因为这个地方跟赋值语句很像,例如“int newAge = age + 10 * 2;”。
理解递归下降算法中的回溯
不知道你有没有发现,我在设计语法规则的过程中,其实故意设计了一个陷阱,这个陷阱能帮我们更好地理解递归下降算法的一个特点:回溯。理解这个特点能帮助你更清晰地理解递归下降算法的执行过程,从而再去想办法优化它。
考虑一下 age = 45;这个语句。肉眼看过去,你马上知道它是个赋值语句,但是当我们用算法去做模式匹配时,就会发生一些特殊的情况。看一下我们对 statement 语句的定义:
我们首先尝试 intDeclaration,但是 age = 45;语句不是以 int 开头的,所以这个尝试会返回 null。然后我们接着尝试 expressionStatement,看一眼下面的算法:
出现了什么情况呢?age = 45;语句最左边是一个标识符。根据我们的语法规则,标识符是一个合法的 addtiveExpresion,因此 additive() 函数返回一个非空值。接下来,后面应该扫描到一个分号才对,但是显然不是,标识符后面跟的是等号,这证明模式匹配失败。
失败了该怎么办呢?我们的算法一定要把 Token 流的指针拨回到原来的位置,就像一切都没发生过一样。因为我们不知道 addtive() 这个函数往下尝试了多少步,因为它可能是一个很复杂的表达式,消耗掉了很多个 Token,所以我们必须记下算法开始时候的位置,并在失败时回到这个位置。尝试一个规则不成功之后,恢复到原样,再去尝试另外的规则,这个现象就叫做“回溯”。
因为有可能需要回溯,所以递归下降算法有时会做一些无用功。在 assignmentStatement 的算法中,我们就通过 unread(),回溯了一个 Token。而在 expressionStatement 中,我们不确定要回溯几步,只好提前记下初始位置。匹配 expressionStatement 失败后,算法去尝试匹配 assignmentStatement。这次获得了成功。
试探和回溯的过程,是递归下降算法的一个典型特征。通过上面的例子,你应该对这个典型特征有了更清晰的理解。递归下降算法虽然简单,但它通过试探和回溯,却总是可以把正确的语法匹配出来,这就是它的强大之处。当然,缺点是回溯会拉低一点儿效率。但我们可以在这个基础上进行改进和优化,实现带有预测分析的递归下降,以及非递归的预测分析。有了对递归下降算法的清晰理解,我们去学习其他的语法分析算法的时候,也会理解得更快。
我们接着再讲回溯牵扯出的另一个问题:什么时候该回溯,什么时候该提示语法错误?
大家在阅读示例代码的过程中,应该发现里面有一些错误处理的代码,并抛出了异常。比如在赋值语句中,如果等号后面没有成功匹配一个加法表达式,我们认为这个语法是错的。因为在我们的语法中,等号后面只能跟表达式,没有别的可能性。
你可能会意识到一个问题,当我们在算法中匹配不成功的时候,我们前面说的是应该回溯呀,应该再去尝试其他可能性呀,为什么在这里报错了呢?换句话说,什么时候该回溯,什么时候该提示这里发生了语法错误呢?
其实这两种方法最后的结果是一样的。我们提示语法错误的时候,是说我们知道已经没有其他可能的匹配选项了,不需要浪费时间去回溯。就比如,在我们的语法中,等号后面必然跟表达式,否则就一定是语法错误。你在这里不报语法错误,等试探完其他所有选项后,还是需要报语法错误。所以说,提前报语法错误,实际上是我们写算法时的一种优化。
在写编译程序的时候,我们不仅仅要能够解析正确的语法,还要尽可能针对语法错误提供友好的提示,帮助用户迅速定位错误。错误定位越是准确、提示越是友好,我们就越喜欢它。
好了,到目前为止,已经能够能够处理几种不同的语句,如变量声明语句,赋值语句、表达式语句,那么我们把所有这些成果放到一起,来体会一下使用自己的脚本语言的乐趣吧!
我们需要一个交互式的界面来输入程序,并执行程序,这个交互式的界面就叫做REPL。
实现一个简单的 REPL
脚本语言一般都会提供一个命令行窗口,让你输入一条一条的语句,马上解释执行它,并得到输出结果,比如 Node.js、Python 等都提供了这样的界面。这个输入、执行、打印的循环过程就叫做 REPL(Read-Eval-Print Loop)。你可以在 REPL 中迅速试验各种语句,REPL 即时反馈的特征会让你乐趣无穷。所以,即使是非常资深的程序员,也会经常用 REPL 来验证自己的一些思路,它相当于一个语言的 PlayGround(游戏场),是个必不可少的工具。
在 SimpleScript.java 中,我们也实现了一个简单的 REPL。基本上就是从终端一行行的读入代码,当遇到分号的时候,就解释执行,代码如下:
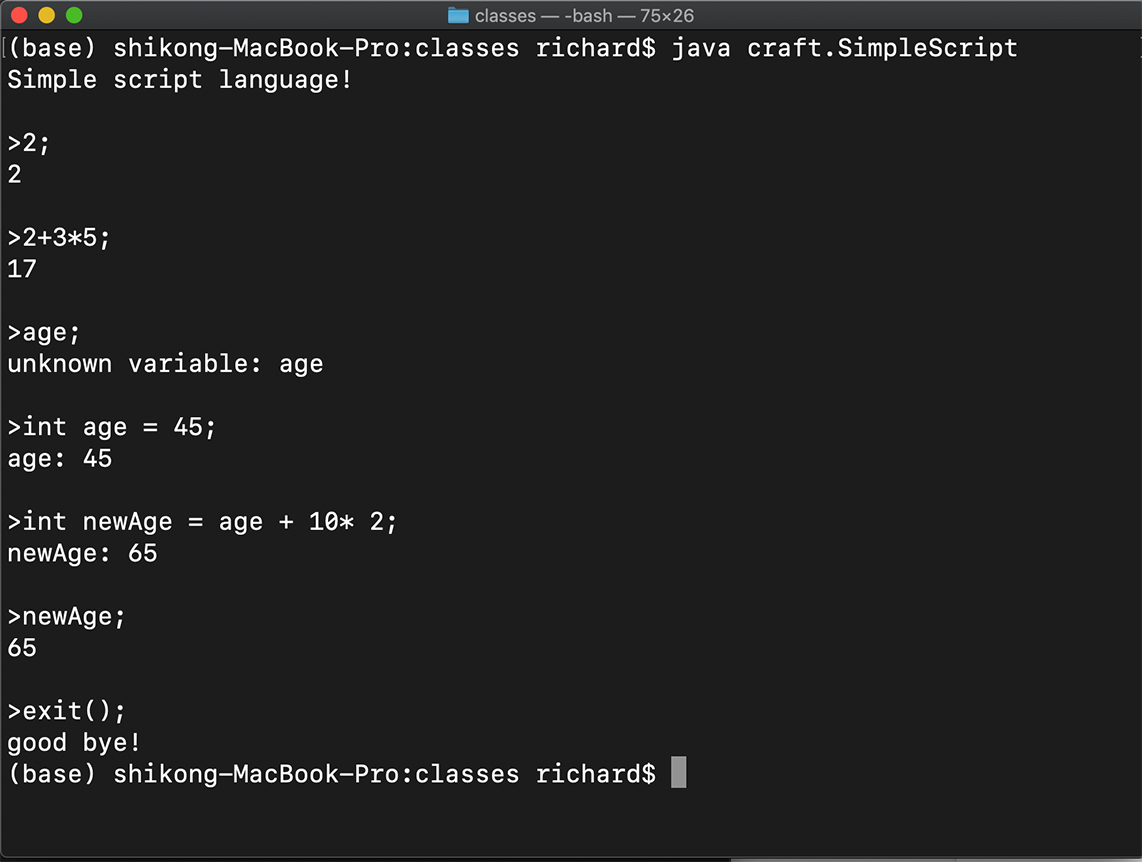
运行 java craft.SimpleScript,你就可以在终端里尝试各种语句了。如果是正确的语句,系统马上会反馈回结果。如果是错误的语句,REPL 还能反馈回错误信息,并且能够继续处理下面的语句。我们前面添加的处理语法错误的代码,现在起到了作用!下面是在我电脑上的运行情况:
如果你用 java craft.SimpleScript -v 启动 REPL,则进入 Verbose 模式,它还会每次打印出 AST,你可以尝试一下。
退出 REPL 需要在终端输入 ctl+c,或者调用 exit() 函数。我们目前的解释器并没有支持函数,所以我们是在 REPL 里硬编码来实现 exit() 函数的。后面的课程里,我会带你真正地实现函数特性。
我希望你能编译一下这个程序,好好的玩一玩它,然后再修改一下源代码,增加一些你感兴趣的特性。我们学习跟打游戏一样,好玩、有趣才能驱动我们不停地学下去,一步步升级打怪。我个人觉得,我们作为软件工程师,拿出一些时间来写点儿有趣的东西作为消遣,乐趣和成就感也是很高的,况且还能提高水平。
课程小结
本节课我们通过对三种语句的支持,实现了一个简单的脚本语言。REPL 运行代码的时候,你会有一种真真实实的感觉,这确实是一门脚本语言了,虽然它没做性能的优化,但你运行的时候也还觉得挺流畅。
学完这讲以后,你也能找到了一点感觉:Shell 脚本也好,PHP 也好,JavaScript 也好,Python 也好,其实都可以这样写出来。
回顾过去几讲,你已经可以分析词法、语法、进行计算,还解决了左递归、优先级、结合性的问题。甚至,你还能处理语法错误,让脚本解释器不会因为输入错误而崩溃。
想必这个时候你已经开始相信我的承诺了:每个人都可以写一个编译器。这其实也是我最想达到的效果。相信自己,只要你不给自己设限,不设置玻璃天花板,其实你能够做出很多让自己惊讶、让自己骄傲的成就。
收获对自己的信心,掌握编译技术,将是你学习这门课程后最大的收获!
一课一思
本节课,我们设计了一个可能导致递归下降算法中回溯的情景。在你的计算机语言中,有哪些语法在运用递归下降算法的时候,也是会导致回溯的?
如果你还想进一步挑战自己,可以琢磨一下,递归下降算法的回溯,会导致多少计算时间的浪费?跟代码长度是线性关系还是指数关系?我们在后面梳理算法的时候,会涉及到这个问题。
欢迎在留言区里分享你的发现,与大家一起讨论。最后,感谢你的阅读,如果这篇文章让你有所收获,也欢迎你将它分享给更多的朋友。
另外,第 2 讲到第 5 讲的代码,都在代码库中的 lab 子目录的 craft 子目录下,代码库在码云和GitHub上都有,希望你能下载玩一玩。
精选留言(10)
- 安排2019-08-24有点感觉了,哈哈😄展开
作者回复: 加油!
1 - 中年男子2019-08-25有了前几讲的基础,这一讲很轻松搞定,根据宫老师的java代码我实现了C++版本,其中一些不太清晰的概念通过代码也理解了,老师真的很棒!展开
作者回复: 谢谢肯定!
编译原理这门课,是学原理可能学不懂。但真正动手,其实都能写出来。早期写编译器的先驱并没有编译原理课。
并且,很多具体实现过程,是可以偏离死搬教条的原理的。比如,理想情况下要设计无二义性文法。实际应用中,只要针对某个具体算法是无二义的就行了。能实际有用才是硬道理。 - LDxy2019-08-24正则表达式匹配文本的时候也会导致回溯吧?好像还有可能因此导致严重的性能问题
作者回复: 对。如果正则表达式的内部实现是基于NFA的,就会有这个问题。
NFA和DFA这个知识点不适合在前期讲,会把初学者搞晕。我准备在后面找个机会放入这个知识点。 - catplanet2019-08-24根据老师讲解,实现了一个 golang 的版本 https://repl.it/@catplanet007/simple-interpreter
作者回复: 你用的这个在线工具很酷。可以提供一个运行环境直接跑!很棒!
我玩了好一会 :-D - wj2019-08-24老师, 还有个问题, 借此文问一下, 词法分析\语法分析等和机器学习有什么交集吗? 我有个场景想比较两个java文件的匹配度, 或者两段代码的匹配度, 不知道机器学习在这个场景是否可以应用, 以及如何应用呢?谢谢~
作者回复: 你提了一个好问题。
其实,人工智能的发展史经历了两个不同的路径。 早期,更多的是演绎逻辑。就是人为制定规则,比如自然语言翻译的规则,并不断执行这些规则。
第二条路径,是最近复兴的机器学习的方法。它更多的是归纳逻辑。机器学习是通过数据的训练,把规则归纳出来。这些归纳出来的规则目前还是比较黑盒的,人比较难以解读,但却很有用,更加准确。
你的需求场景用这两种方法应该都能解决,只不过落地时还要考虑很多细节和限制因素。 - wj2019-08-24老师, 我发现对一些基本术语, 比如 Statement, expression, binaryExpression, 等不太会分辨, 请问有什么书或资料可以推荐系统看一下吗? 谢谢展开
作者回复: 可以参考成熟的语法规则文件,去琢磨。
大致来说,你从字面意思来理解它就好了。比如语句、表达式、二元表达式。
本课程都是倾向于采用这种有意义的单词,而不是像教科书那样只写一个字母,太抽象。
而在实际工程中,我们总是让自己的语法单元更具可读性,这样更实用。 - 沉淀的梦想2019-08-23Java中的范型语法应该是需要回溯的。感觉计算时间的浪费和代码长度应该是指数关系。
作者回复: 为你的动脑思考点赞!
泛型语法,嗯嗯有可能。
深度优先算法的回溯,时间复杂性(大O)不是指数的。广度优先的才是指数的。这个在15讲会再总结一遍。
深度优先算法,实际浪费不多,所以是有实用价值的一个算法。再加上预测功能就完美了。讲LL算法的时候会再回过来说这个事情。 - 许童童2019-08-23老师讲得好啊,不要给自己设天花板,不断努力,成功最终会属于你。
作者回复: 是的。
很多时候,做某件事情真正的阻力是畏惧,是根本不去做... - 雲至2019-08-23老师 那个verbase是什么意思呀展开
作者回复: 是verbose吧?也就是启动“话痨”模式,打印输出等多信息。
有一些linux命令习惯上会用-v参数来表达这个意思 :-D 1 - 雲至2019-08-23老师 那个verbase是什么变量呀展开